Reflective Holographic Gratings
- Free from Random Spacing Errors
- Optimized for the UV and Visible Spectrum
- 45% to 65% Efficiencies
GH50-12V
GH25-06U
GH13-06U

Please Wait
| Selection Guide | |
|---|---|
| Reflective Gratings | |
| Ruled | UV |
| Visible | |
| Near IR | |
| Mid IR | |
| Holographic | |
| Echelle | |
| Transmission Gratings | |
| UV | |
| Visible | |
| Near IR | |
Features
- 45% to 65% Efficiencies at Peak Wavelength
- Versions Optimized for the UV and Visible Spectrum
- Relatively Independent of Angle of Incidence
- Substrate: Borofloat
- Three Sizes: 12.7 x 12.7 x 6.0 mm, 25 x 25 x 6.0 mm, and 50 x 50 x 9.5 mm
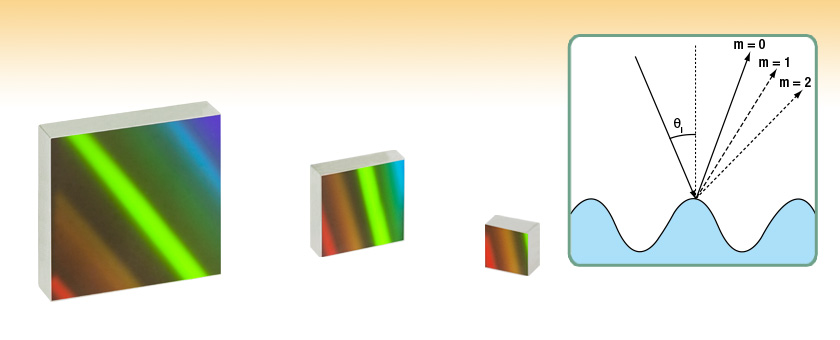
Thorlabs offers a selection of holographic diffraction gratings optimized for high end applications that require a high signal to noise ratio. Holographic gratings feature low stray light, which nearly eliminates all ghosting that ruled gratings suffer from and makes them an ideal solution for applications such as Raman spectroscopy that require high signal to noise ratios. Our holographic gratings are optimized for the UV or Visible spectral ranges and are available in three sizes with groove densities from 600 to 3600 lines/mm. For more information on selecting the right type of grating for your application, please see the Gratings Guide tab above.
Mounts and Adapters
Thorlabs offers a variety of mounts and adapters for precise and stable mounting and aligning square optics. All of Thorlabs' gratings can be mounted directly into the KM100C Right-Handed or KM100CL Left-Handed Kinematic Rectangular Optic Mount. Gratings can also be mounted in one of three Kinematic Grating Mount Adapters which can be used with any of Thorlabs' Ø1" Mirror Mounts, including the POLARIS-K1 Ultra-Stable Kinematic Mirror Mount.
Warning:
Optical gratings can be easily damaged by moisture, fingerprints, aerosols, or the slightest contact with any abrasive material. Gratings should only be handled when necessary and always held by the sides. Latex gloves or a similar protective covering should be worn to prevent oil from fingers from reaching the grating surface. No attempt should be made to clean a grating other than blowing off dust with clean, dry air or nitrogen. Solvents will likely damage the grating's surface.
Thorlabs uses a clean room facility for assembly of gratings into mechanical setups. If your application requires integrating the grating into a sub-assembly or a setup, please contact Tech Support to learn more about our assembly capabilities.
Diffraction Gratings Tutorial
Diffraction gratings, either transmissive or reflective, can separate different wavelengths of light using a repetitive structure embedded within the grating. The structure affects the amplitude and/or phase of the incident wave, causing interference in the output wave. In the transmissive case, the repetitive structure can be thought of as many tightly spaced, thin slits. Solving for the irradiance as a function wavelength and position of this multi-slit situation, we get a general expression that can be applied to all diffractive gratings when = 0°,

(1)
known as the grating equation. The equation states that a diffraction grating with spacing will deflect light at discrete angles (
), dependent upon the value
λ, where
is the order of principal maxima. The diffracted angle,
, is the output angle as measured from the surface normal of the diffraction grating. It is easily observed from Eq. 1 that for a given order
, different wavelengths of light will exit the grating at different angles. For white light sources, this corresponds to a continuous, angle-dependent spectrum.

Figure 1. Transmission Grating
Transmission Gratings
One popular style of grating is the transmission grating. This type of diffraction grating is created by scratching or etching a transparent substrate with a repetitive, parallel structure. This structure creates areas where light can scatter. A sample transmission grating is shown in Figure 1.
The transmission grating, shown in Figure 1, is comprised of a repetitive series of narrow-width grooves separated by distance . The incident light impinges on the grating at an angle
, as measured from the surface normal. The light of order
exiting the grating leaves at an angle of
, relative to the surface normal. Utilizing some geometric conversions and the general grating expression (Eq. 1) an expression for the transmissive diffraction grating can be found:

(2)
where both and
are positive if the incident and diffracted beams are on opposite sides of the grating surface normal, as illustrated in the example in Figure 1. If they are on the same side of the grating normal,
must then be considered negative.

Figure 2. Reflective Grating
Reflective Gratings
Another very common diffractive optic is the reflective grating. A reflective grating is traditionally made by depositing a metallic coating on an optic and ruling parallel grooves in the surface. Reflective gratings can also be made of epoxy and/or plastic imprints from a master copy. In all cases, light is reflected off of the ruled surface at different angles corresponding to different orders and wavelengths. An example of a reflective grating is shown in Figure 2. Using a similar geometric setup as above, the grating equation for reflective gratings can be found:

(3)
where is positive and
is negative if the incident and diffracted beams are on opposite sides of the grating surface normal, as illustrated in the example in Figure 2. If the beams are on the same side of the grating normal, then both angles are considered positive.
Both the reflective and transmission gratings suffer from the fact that the zeroth order mode contains no diffraction pattern and appears as a surface reflection or transmission, respectively. Solving Eq. 2 for this condition, =
, we find the only solution to be
=0, independent of wavelength or diffraction grating spacing. At this condition, no wavelength-dependent information can be obtained, and all the light is lost to surface reflection or transmission.
This issue can be resolved by creating a repeating surface pattern, which produces a different surface reflection geometry. Diffraction gratings of this type are commonly referred to as blazed (or ruled) gratings. An example of this repeating surface structure is shown in Figure 3.
Blazed (Ruled) Gratings

Figure 4. Blazed Grating, 0th Order Reflection

Figure 3. Blazed Grating Geometry
The blazed grating, also known as the echelette grating, is a specific form of reflective or transmission diffraction grating designed to produce the maximum grating efficiency in a specific diffraction order. This means that the majority of the optical power will be in the designed diffraction order while minimizing power lost to other orders (particularly the zeroth). Due to this design, a blazed grating operates at a specific wavelength, known as the blaze wavelength.
The blaze wavelength is one of the three main characteristics of the blazed grating. The other two, shown in Figure 3, are , the groove or facet spacing, and
, the blaze angle. The blaze angle
is the angle between the surface structure and the surface parallel. It is also the angle between the surface normal and the facet normal.
The blazed grating features geometries similar to the transmission and reflection gratings discussed thus far; the incident angle () and
th order reflection angles (
) are determined from the surface normal of the grating. However, the significant difference is the specular reflection geometry is dependent on the blaze angle,
, and NOT the grating surface normal. This results in the ability to change the diffraction efficiency by only changing the blaze angle of the diffraction grating.
The 0th order reflection from a blazed grating is shown in Figure 4. The incident light at angle is reflected at
for
= 0. From Eq. 3, the only solution is
= –
. This is analogous to specular reflection from a flat surface.

Figure 6. Blazed Grating, Incident Light Normal to Grating Surface

Figure 5. Blazed Grating, Specular Reflection from Facet
The specular reflection from the blazed grating is different from the flat surface due to the surface structure, as shown in Figure 5. The specular reflection, , from a blazed grating occurs at the blaze angle geometry. This angle is defined as being negative if it is on the same side of the grating surface normal as
. Performing some simple geometric conversions, one finds that

(4)
Figure 6 illustrates the specific case where = 0°, hence the incident light beam is perpendicular to the grating surface. In this case, the 0th order reflection also lies at 0°. Utilizing Eqs. 3 and 4, we can find the grating equation at twice the blaze angle:

(5)
Littrow Configuration
The Littrow configuration refers to a specific geometry for blazed gratings and plays an important role in monochromators and spectrometers. It is the angle at which the grating efficiency is the highest. In this configuration, the angle of incidence of the incoming and diffracted light are the same,
=
, and
> 0 so

(6)

Figure 7. Littrow Configuration
The Littrow configuration angle, , is dependent on the most intense order (
= 1), the design wavelength,
, and the grating spacing
. It is easily shown that the Littrow configuration angle,
, is equal to the blaze angle,
, at the design wavelength. The Littrow / blaze angles for all Thorlabs' Blazed Gratings can be found in the grating specs tables.

(7)
It is easily observed that the wavelength dependent angular separation increases as the diffracted order increases for light of normal incidence (for = 0°,
increases as
increases). There are two main drawbacks for using a higher order diffraction pattern over a low order one: (1) a decrease in efficiency at higher orders and (2) a decrease in the free spectral range,
![]() , defined as:
, defined as:

(8)
where is the central wavelength, and
is the order.
The first issue with using higher order diffraction patterns is solved by using an Echelle grating, which is a special type of ruled diffraction grating with an extremely high blaze angle and relatively low groove density. The high blaze angle is well suited for concentrating the energy in the higher order diffraction modes. The second issue is solved by using another optical element: grating, dispersive prism, or other dispersive optic, to sort the wavelengths/orders after the Echelle grating.

Figure 8. Holographic Grating
Holographic Surface Gratings
While blazed gratings offer extremely high efficiencies at the design wavelength, they suffer from periodic errors, such as ghosting, and relatively high amounts of scattered light, which could negatively affect sensitive measurements. Holographic gratings are designed specially to reduce or eliminate these errors. The drawback of holographic gratings compared to blazed gratings is reduced efficiency.
Holographic gratings are made from master gratings by similar processes to the ruled grating. The master holographic gratings are typically made by exposing photosensitive material to two interfering laser beams. The interference pattern is exposed in a periodic pattern on the surface, which can then be physically or chemically treated to expose a sinusoidal surface pattern. An example of a holographic grating is shown in Figure 8.
Please note that dispersion is based solely on the number of grooves per mm and not the shape of the grooves. Hence, the same grating equation can be used to calculate angles for holographic as well as ruled blazed gratings.
Reflective Gratings
Reflective grating master copies are made by depositing a metallic coating on an optic and ruling parallel grooves in the surface. Thorlabs' reflective gratings are made of epoxy and/or plastic imprints from a master copy, in a process call replication. In all cases, light is reflected off of the ruled surface at different angles corresponding to different orders and wavelengths. All of Thorlabs' ruled reflective diffraction gratings exhibit a sawtooth profile, also known as blazed, while our reflective holographic diffraction gratings exhibit a sinusoidal profile. For more information, please refer to the Gratings Tutorial tab.
| Ruled Diffraction Gratings | |||
|---|---|---|---|
 |
Ruled | UV | Ruled gratings can achieve higher efficiencies than holographic gratings due to their blaze angles. They are ideal for applications centered near the blaze wavelength. Thorlabs offers replicated ruled diffraction gratings in a variety of sizes and blaze angles. |
| Visible | |||
| Near IR | |||
| Mid IR | |||
| UV Ruled Reflective Blazed Diffraction Gratings |
|---|
| Visible Ruled Reflective Blazed Diffraction Gratings |
|---|
| Near-IR Ruled Reflective Blazed Diffraction Gratings |
|---|
| Mid-IR Ruled Reflective Blazed Diffraction Gratings |
|---|
| Holographic Diffraction Gratings | |||
|---|---|---|---|
 |
Holographic | Holographic gratings have a low occurrence of periodic errors, which results in limited ghosting, unlike ruled gratings. The low stray light of these gratings makes them ideal for applications where the signal-to-noise ratio is critical, such as Raman Spectroscopy. | |
| Reflective Holographic Sinusoidal Diffraction Gratings |
|---|
| Echelle Diffraction Gratings | |||
|---|---|---|---|
 |
Echelle | Echelle gratings are low period gratings designed for use in high diffraction orders. They are generally used with a second grating or prism to separate overlapping diffracted orders. They are ideal for applications such as high-resolution spectroscopy. | |
| Echelle Ruled Blazed Diffraction Gratings |
|---|
Transmission Gratings
Transmission gratings are created by scratching or etching a transparent substrate with a repetitive, parallel structure. This structure creates areas where light can scatter. Thorlabs' transmission gratings are manufactured using the ruled method, which creates a sawtooth diffraction profile. Transmission gratings can also be made of epoxy and/or plastic imprints from a master copy, in a process call replication. For more information, please refer to the Gratings Tutorial tab.
| Transmission Diffraction Gratings | |||
|---|---|---|---|
 |
UV | Thorlabs' transmission gratings disperse incident light on the opposite side of the grating at a fixed angle. They are ruled and blazed for optimum efficiency in their respective wavelength range, are relatively polarization insensitive, and have an efficiency comparable to that of a reflection grating optimized for the same wavelength. They are ideal for applications that require fixed gratings such as spectrographs. | |
| Visible | |||
| Near IR | |||
| UV Transmission Blazed Diffraction Gratings |
|---|
| Visible Transmission Blazed Diffraction Gratings |
|---|
| NIR Transmission Blazed Diffraction Gratings |
|---|
Selecting a grating requires consideration of a number of factors, some of which are listed below:
Efficiency:
Ruled gratings generally have a higher efficiency than holographic gratings. Holographic grating tend to have a lower efficiency but a broader effective wavelength range. The efficiency of ruled gratings may be desirable in applications such as fluorescence excitation and other radiation-induced reactions.
Blaze Wavelength:
Ruled gratings have a sawtooth groove profile created by sequentially etching the surface of the grating substrate. As a result, they have a sharp peak efficiency around their blaze wavelength. Holographic gratings are harder to blaze, and tend to have a sinusoidal groove profile resulting in a less intense peak around the design wavelength. Applications centered around a narrow wavelength range could benefit from a ruled grating blazed at that wavelength.
Stray Light:
Due to a difference in how the grooves are made, holographic gratings have less stray light than ruled gratings. The grooves on a ruled grating are machined one at a time which results in a higher frequency of errors. Holographic gratings are made through a lithographic process, which generally creates smoother grating masters free of tool marks. Replicants made from these masters exhibit less stray light. Applications such as Raman spectroscopy, where signal-to-noise is critical, can benefit from the limited stray light of the holographic grating.
Resolving Power:
The resolving power of a grating is a measure of its ability to spatially separate two wavelengths. It is determined by applying the Rayleigh criteria to the diffraction maxima; two wavelengths are resolvable when the maxima of one wavelength coincides with the minima of the second wavelength. The chromatic resolving power (R) is defined by R = λ/Δλ = n*N, where Δλ is the resolvable wavelength difference, n is the diffraction order, and N is the number of grooves illuminated. Due to their low groove density, Echelle gratings provide high resolving power.
For further information about gratings and selecting the grating right for your application, please visit our Gratings Tutorial.
Caution:
The surface of a diffraction grating can be easily damaged by fingerprints, aerosols, moisture or the slightest contact with any abrasive material. Gratings should only be handled when necessary and always held by the sides. Latex gloves or a similar protective covering should be worn to prevent oil from fingers from reaching the grating surface. Solvents will likely damage the grating's surface. No attempt should be made to clean a grating other than blowing off dust with clean, dry air or nitrogen. Scratches or other minor cosmetic imperfections on the surface of a grating do not usually affect performance and are not considered defects.
| Posted Comments: | |
Chirag Patel
(posted 2020-04-07 05:58:22.76) We are using optical emissions spectrometer, make: GNR Italy
Model: Solaris CCD Plus
By mistake our technician clean the griting with tissue so we are not getting proper results,
So please guide us what we have to do. YLohia
(posted 2020-04-07 09:22:04.0) Thank you for contacting Thorlabs. We recommend following the general optics cleaning guide: https://www.thorlabs.com/newgrouppage9.cfm?objectgroup_id=9025. I will reach out to you directly to discuss your issues. Tyler
(posted 2008-07-29 15:35:41.0) A response from Tyler at Thorlabs to phybmd: Thank you for your interest in our products. An applications engineer will be contacting you to gather more information about your application in order to determine the feasibility of adding this size grating to our product line. They will also provide a custom quote for producing the product you requested. phybmd
(posted 2008-07-27 20:59:54.0) We use the diffraction gratings in a diode laser setup (and I would imagine so would many others). To facilitate better design it would be extremely useful to have custom substrate sizes. I would prefer 12.7mm x 6.35mm x 3mm (grating is at 45 degrees to the laser beam). Any possibility that gratings could be made on different substrates? |


 Products Home
Products Home











 Zoom
Zoom
 Holographic Reflective Gratings
Holographic Reflective Gratings